How to Build a Highly Available System
Without a Toolkit
Butler Lampson
Abstract: In this talk I will describe the general recipe for building a highly available system and show how to do it efficiently in practice. The idea is to build a replicated state machine. The tricky part is getting all the replicas to agree on the content and order of the inputs. For this you need a general fault-tolerant algorithm for reaching consensus. Two-phase commit uses the simplest possible such algorithm, but I will describe Lamport's "Paxos" algorithm, which is the best one that works without real-time guarantees. Since consensus is expensive, you also need to minimize its use, and you do that with leases, which are locks that time out.
The other theme of the talk is a general method for designing or understanding a complex system, especially a concurrent or fault-tolerant one. Using the Paxos algorithm as the example, I will show you how to write a precise spec for such a system and how to prove that an implementation satisfies the spec. There won't be any formulas in the talk.
What This Talk is About
How to build a highly available system using consensus.
Availability is not having to say “I’m sorry”.
A
distributed system is a system in which I can’t do my work because some
computer has failed that I’ve never even heard of.
Lamport
The most fault-tolerant algorithm for consensus without real-time guarantees.
Lamport’s “Paxos” algorithm.
How to design and understand a concurrent, fault-tolerant system.
Highly Available Computing
High availability means either perfection or redundancy.
The system can work even when some parts are broken.
The simplest redundancy is replication:
Several copies of each part.
Each non-faulty copy does the same thing.
Every computing system works as a state machine.
So a replicated state machine can do highly available computing.
This idea is due to Leslie Lamport.
Replicated State Machines
If a state machine is deterministic, then feeding two copies the same inputs will produce the same outputs and states.
We call each copy a process.
So all we need is to agree on the inputs.
Examples:
Replicated storage with Read(a) and Write(a, d) steps.
Airplane flight control system with ReadInstrument(i) and RaiseFlaps(d) steps.
Agreeing on some value is called consensus.
A replicated state machine needs to agree on a sequence of values:
Input 1 Write(x, 3)
Input 2 Read(x)
. . .
Simple Implementations of Consensus
A single process, with the same state as the specification, tells everyone else the outcome (two-phase commit works this way).
This is not fault-tolerant — it fails if the coordinator fails.
A set of processes, each choosing a value. If a majority choose the same value, that is the outcome.
This is not fault-tolerant — it fails if a majority doesn’t agree, or if a member of the majority fails.
Efficient Highly Available Computing
Fault-tolerant consensus is expensive.
Exclusive access (locking) is cheap, but not fault-tolerant.
Leases are “fault-tolerant” locks, which time out.
Like ordinary locks, leases can be hierarchical.
Only the root lease need be granted by consensus.
Leases: Fault-Tolerant Locks
Consider a synchronous system: processes have clocks with bounded skew.
Run consensus to issue a lease on some component x of the state.
The lease expires at a stated time.
The lease is granted to a process which becomes the master for x.
During the period of the lease, the master can read and write x freely.
Writes of x must take bounded time, so they end before the lease expires.
If the master fails, x is inaccessible until the lease expires.
Run consensus again to renew the lease.
Tradeoff: Short lease means quick
recovery but more cost to renew lease.
Long lease means
slow
recovery but less cost to
renew lease.
Examples:
x is a multi-ported disk
x is a cache block
Hierarchical Leases
Problem:
Running consensus to issue a lease is too expensive.
Solution:
Run consensus once to elect a czar C and give C a lease.
Now C gives out sub-leases on x and y to masters.
Each master controls its part of the state.
The masters renew their sub-leases with the czar. This is cheap.
The czar renews its lease by consensus. This costs more, but there’s only one czar lease.
Also, the czar can be simple and less likely to fail, so a longer lease may be OK.
This method is commonly used in replicated file systems and in clusters.
Consensus
Several processes (or computers) achieve consensus if they all agree on some value.
Consensus is tricky when there are faults.
In an asynchronous system with a single faulty process, there is no algorithm for consensus that is guaranteed to terminate (Fisher-Lynch-Paterson).
In a synchronous system consensus is possible even with processes that have arbitrary or malicious faults (Byzantine agreement), but it is expensive in messages sent and in time.
Other applications of consensus
Committing a distributed transaction: agree on commit or abort.
Electing a leader: agree on the new leader.
Group membership: agree on current members.
Specifying a System with State
We only care about the sequence of external actions.
You can’t observe the actual state of the system from outside.
The properties of a sequence of actions:
A safety property: nothing bad ever
happens.
Easily defined by a state
machine:
state: a set of values, usually divided into named variables.
actions: named changes in the state; internal and external.
A liveness property: something good eventually happens.
These two define behavior: all the possible sequence of actions.
Examples of systems with state:
Data abstractions
Concurrent systems
Distributed systems
What “Implements” Means
Y implements X if
every external behavior of Y is an external behavior of X, and
Y’s liveness property implies X’s liveness property.
This expresses the idea that Y
implements X if
you can’t tell Y apart from X by looking only at the external actions.
How to Write a Spec
Figure out what the state is.
Choose the state to make the spec clear, not to match the code.
Describe the actions.
What they do to the state.
What they return.
Helpful hints
Notation is important, because it helps you to think about what’s going on.
Invent a suitable vocabulary.
Less is more. Fewer actions are better.
More non-determinism is better, because it allows more implementations.
I’m sorry I wrote you such a long letter; I didn’t have time to write a short
one. Pascal
Specification for Consensus
State:
outcome : Value È {nil} initially nil
|
Name |
Guard |
Effect |
|
allow(v) |
|
choose
if outcome = nil then outcome := v |
|
outcome |
|
choose
return outcome |
Terminating Consensus
State:
outcome : Value È {nil} initially
nil
done :
Bool initially false
|
Name |
Guard |
Effect |
|
allow(v) |
|
choose
if outcome = nil then outcome := v |
|
outcome |
|
choose
return outcome |
|
|
|
|
|
terminate |
outcome ¹ nil |
done := true |
Deferred Consensus
State:
outcome : Value È {nil} initially nil
done :
Bool initially false
allowed : set Value initially {}
|
Name |
Guard |
Effect |
|
allow(v) |
|
allowed := allowed È {v} |
|
outcome |
|
choose
return outcome |
|
|
|
|
|
agree(v) |
outcome = nil |
outcome := v |
|
terminate |
outcome ¹ nil |
done := true |
Proving that Y implements X
Define an abstraction function f from the state of Y to the state of X.
Show that Y simulates X:
1) f maps initial states of Y to initial states of X.
![]()
![]()
![]() 2) For
each Y-action and each state y
2) For
each Y-action and each state y
there is a sequence of X-actions that is the same externally,
such that the diagram commutes.
![]()
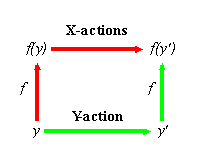
This always works!
Invariants describe the reachable states of Y; simulation only needs to work from a reachable state.
Abstraction Functions for
Simple Implementations
A single coordinator process, with the same state as the specification, tells everyone else the outcome (this is how two-phase commit works). The abstraction function is:
outcome = the outcome of the coordinator.
done = everyone has gotten the outcome.
This is not fault-tolerant — it fails if the coordinator fails.
A set of processes, each choosing a value. If a majority choose the same value, that is the outcome. The abstraction function is:
outcome = the choice of
a majority, or nil if there’s no majority.
This is not fault-tolerant — it fails if a majority doesn’t agree, or if a member of the majority fails.
How to Design an Implementation
Write the specification first.
Dream up the idea of the implementation.
Embody the key idea in the abstraction function.
Check that each implementation action simulates some spec actions.
Add invariants to make this easier. Each action must maintain them.
Change the implementation (or the spec) until this works.
Make the implementation correct first, then efficient.
More efficiency means more complicated invariants.
You might need to change the spec to get an efficient implementation.
An efficient program is an exercise in logical brinksmanship
Dijkstra
A Fault-Tolerant Implementation: Ideas
A set of agent processes, indexed by I. The agents do what they are told.
Agents have “persistent” storage that survives crashes.
Some leader processes that tell the agents what to do.
A set of
rounds, indexed by N. Each round has at most one value vn.
In each round, some of the agents may
accept the value.
If a majority accept, that value is the
outcome.
Two majorities always intersect.
An algorithm based on this idea was invented by Leslie Lamport, who called it “Paxos”, and independently by Liskov and Oki as part of a replicated storage system.
Agent State
The state of the agents is the persistent variables (for the moment, don’t worry about how to code this efficiently):
si, n : Value È {no, neutral} initially neutral
A state component can only change if it is neutral.
Define the value of round n:
vn º if
some agent i has a Value in si, n then si, n
else nil
Invariant 1: A round has at most one value.
That is, in a given round all the agents with a value have the same value.
The abstraction function is
outcome = vn for some round n that has a
majority for vn,
or nil if there is no
such n
Invariant 2: If two rounds have majorities for a value, it is the same value.
Stable Predicates
A predicate P is stable º once true, P is true henceforth º P Þ q P
This is important because it’s safe to act on the truth of a stable predicate. Anything else might change because of concurrency or crashes.
These predicates are stable:
si, n = no
si, n = v
vn = v
n is dead º round n has a majority for no
n is successful º round n has a majority for some value
n is anchored º for all m £ n, m
is dead or vn = vm
For the last, we need a total ordering on N.
Stronger Invariants
Invariant 2: Any two successful rounds have the same value.
which follows from
Invariant 3: for all n and m £ n, if m is successful then vn = nil or vn = vm
which follows from
Invariant 4: for all n and m £ n, if m is not dead then vn = nil or vn = vm
º for all n and m £ n, m is dead or vn = nil or vn = vm
º for all n, vn = nil or (for all m £ n, m is dead or vn = vm)
º for all n, vn = nil or n is anchored
So all we have to do is choose each vn so that
there is only one, and
n is anchored.
Now the rest of the algorithm is obvious.
Leaders
Maintain invariant 1 (a round has at most one value) by having
at most one leader process per round
that keeps the current round and its value in volatile variables
and doesn’t resume an old round after a crash
Let N = (J, L). The ordering is lexicographic.
Leader l chooses (j, l) for n,
where j is a J that l has not used before (for instance, a local clock).
The state of a leader is the volatile variables:
nl :
N È {nil} initially nil
ul : Value È {nil} initially nil
allowedl : set Value initially
{}
The abstraction function is allowed = Èl Î L allowedl
A
crash of leader l sets nl and ul to nil and may set allowedl to {}.
Paxos Algorithm
Maintain invariant 4 by choosing vn to keep n anchored.
|
Leader l |
Message |
Agent
i |
|
Choose a new n |
|
|
|
Query a majority of agents for their status |
query(n)
® |
for all m < n, if
si, m = neutral then si, m := no |
|
|
¬ report(i, si) |
|
|
Choose vn to keep n anchored.
If all m < n are dead, choose any vn in allowedl |
|
|
|
Command
a majority |
command(n, vn) ® |
if
si, n = neutral |
|
|
¬ report(i, n, si, n) |
|
|
If a majority accepts, publish the outcome vn |
outcome(vn) ® |
|
Examples
|
|
Status
|
|
|
|
vn sa, n sb, n sc, n
|
vn sa, n sb, n sc, n
|
Round 1
Round 2
Round 3
|
7 7 no no
9 no no 9
|
8 8 no no 9 9 no 9 9 no no 9 |
Leader’s
|
7, 8, 9 if a, b, c
report 8 if a, b or b, c report 9 if b, c report |
9 no
matter what majority reports |
A successful round acts as a barrier.
Since it isn’t dead, any later round must choose the same value.
When does outcome change in the spec?
When an agent accepts and forms a majority.
But no one
knows that this has happened until later!
Termination: Choosing a Leader
With one leader that doesn’t fail, Paxos terminates when the leader succeeds in both querying and commanding a majority of agents (perhaps not the same majority).
With multiple leaders, Paxos may never terminate, because later queries can make earlier rounds dead before the agents get commands.
Here is a sloppy algorithm for choosing a single leader, if processes have clocks and the usual maximum time to send, receive, and process a message is known:
Every potential leader that is up broadcasts its name.
You become the leader one round-trip time after doing a broadcast unless you have received the broadcast of a bigger name.
Optimizations
The relevant part of si is just the most recent value and the later no states:
si, last = v,
si, m = no for all m between last and next, and
si, m = neutral for all m ³ next.
Encode this as (v, last, next).
For a sequence of consensus problems (for instance, the successive steps of a state machine) we run a sequence of instances of Paxos, numbered by another index p.
Make the state
(v, last, next) for agent i and instance p encode
sq, i, m = no
for all q £ p and m < next.
Then a query only needs to be done once each time the leader changes.
Piggyback the outcome message on the next instance.
The result is 2 messages (1 round trip) for each consensus.
Summary
How to build a highly available system using consensus.
Run a replicated deterministic state machine, and get consensus on each input.
Use leases to replace most of the consensus steps with actions by one process.
The most fault-tolerant algorithm for consensus without real-time guarantees.
Lamport’s “Paxos” algorithm, based on
Repeating rounds until you get a majority.
Ensuring that every round after a majority has the same value.
How to design and understand a concurrent, fault-tolerant system.
Write a simple spec as a state machine.
Find the abstraction function from the implementation to the spec.
Show that the implementation simulates the spec.
References
Specifications Lamport, A simple approach to specifying concurrent systems. Comm acm, 32, 1, Jan. 1989.
Impossibility Fischer, Lynch, and Paterson, Impossibility of distributed consensus with one faulty process. J. acm 32, 2, April 1985.
Paxos algorithm Lamport, The part-time parliament. Technical Report 49, Digital Equipment Corp, Palo Alto, Sep. 1989.
Liskov and Oki,
Viewstamped replication, Proc. 7th PODC, Aug. 1988.
State machines Lamport, Using time instead of timeout for fault-tolerant distributed systems. acm TOPLAS 6, 2, April 1978.
Schneider, Implementing fault-tolerant services using the state-machine approach: A tutorial. Computing Surveys 22 (Dec 1990).
This talk Lampson,
How to build a highly available system using consensus. In Distributed Algorithms, ed. Babaoglu and Marzullo, LNCS 1151, Springer, 1996.
